Iterative Methods
Some Iterative Methods #
Lecture 21: “Iterative Methods for Solving System of Linear Equations” - YouTube
Idea for deriving an iterative method:
$$ \begin{align*} Ax=B\\ (P-N)x=B\\ \text{P is a non singular matrix}\\ Px=Nx+B\\ x^{k+1}=Gx^{k}+HB\\ G: \text{ iteration matrix }=P^{-1}N;H=P^{-1} \end{align*} $$
Gauss Jacobi Method #
It’s an iterative way to find the approximate solution.
First, we have to make sure if the coefficient matrix is “diagonally dominant by rows” $$ |a_{nn}|>|a_{nx}| $$
System of Equations #
$$ \begin{align*} a_{11}x_{1}+a_{12}x_{2}+…+a_{1n}x_{n}=b_{1}\\ a_{21}x_{1}+a_{22}x_{2}+…+a_{2n}x_{n}=b_{2}\\ .\\ .\\ .\\ a_{n1}x_{1}+a_{n2}+…+a_{nn}x_{n}=b_{n} \end{align*} $$
Iteration #
Solving for $x_m$ in terms of other variables from each mᵗʰ equation:
We mark the ’level’ of iteration with a superscript. $$ \begin{align*} x_{1}^{k+1}=\frac{1}{a_{11}}(b_{1}-a_{12}x_{2}^{k}-…-a_{1n}x_{n}^{k})\\ x_{2}^{k+1}=\frac{1}{a_{22}}(b_{2}-a_{21}x_{1}^{k}-…-a_{2n}x_{n}^{k})\\ …\\ x_{n}^{k+1}=\frac{1}{a_{nn}}(b_{n}-a_{n1}x_{1}^{k}…-a_{nn-1}x_{n-1}^{k})\\ \\ \text{matrix form}\\\ Ax=B\\ (L+D+U)x=B\\ Dx=-(L+U)x+B\
\\ x^{k+1}=-D^{-1}(L+U)x^{k}+D^{-1}B \end{align*} $$
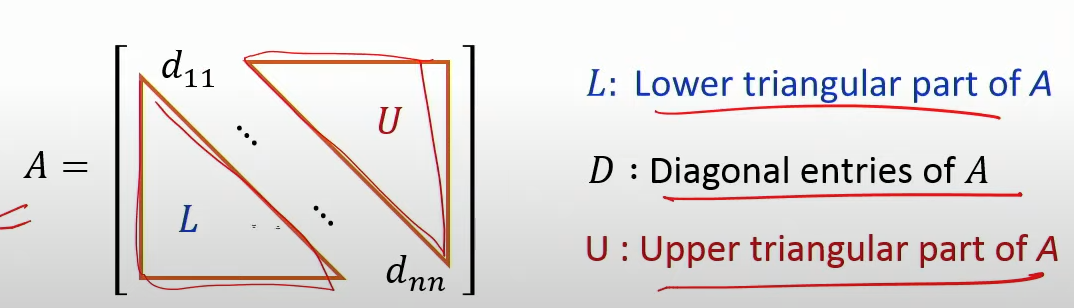 A=L+D+U
A=L+D+U
Can be easily calculated on a Casio 991MS calculator using
[!casio formula] ex: for a system of linear equations in three variables $D\rightarrow0$, $E\rightarrow0$, $F\rightarrow0$ $$A=D:B=E:C=F:D=\frac{1}{a_{11}}(b_{1}-a_{12}B-a_{13}C):E=\frac{1}{a_{22}}(b_{2}-a_{21}A-a_{23}C):F=\frac{1}{a_{33}}(b_{3}-a_{31}A-a_{32}B)$$ A,B,C=$x_{1},x_{2},x_{3}$
and pressing Enter or = multiple times to iterate through successive ‘k’ levels.
Gauss Seidel Method #
Only a minor change compared to
For every $x_{i}^{k+1}$ computation we use the newly computed $x_{j}^{k+1}$ instead of the previous $x_{j}^{k}$ for all j<i and we use the past level value $x_{j}^{k}$ if j>i (from the U block of the matrix)
Iteration matrix here becomes just $(D+L)^{-1}U$ instead of $D^{-1}(L+U)$ fom Gauss Jacobi method since here, only U is used with the previous level (k) for computation of k+1
$$ \begin{align*} Ax=B\\ (L+D+U)x=B\\ (L+D)x=-Ux+B\\ \\ x^{k+1}=-(D+L)^{-1}Ux^{k}+(D+L)^{-1}B \end{align*} $$
This method helps the values converge better.
Convergence #
Lecture 23: “Iterative Methods for Solving System of Linear Equations (Cont.)” - YouTube
The iterative methods converge iff spectral radius (largest absolute eigenvalue) of iteration matrix G is less than 1 ρ(G)<1
We prove this the following way:
- If ρ(G)<1, then:
- $\lim\limits _{m\rightarrow \infty}G^{m}= 0$
- Error goes to 0 and it converges