Rank and solution of linear equations
Rank #
The rank of a matrix is said to be ‘r’ if
- It has atleast 1 non-zero minor of order r
- Every minor of order higher than r is 0.
Some theorems #
A matrix can be made row equivalent to a row echelon matrix by elementary row operations
Rank of a matrix remains invariant under elementary row operations ∴ Rank of a matrix=Number of non-zero rows in Row-reduced echelon form
System of Linear Equations with Matrices #
Given a system of linear equations we can represent it as
$$ Ax=B $$ A: Coefficient Matrix B: Solution Matrix
Augmented Matrix: $\bar A=(A|B)$
Equivalent Systems: $Ax=B$, $Cx=D$ are said to be equivalent systems if the corresponding augmented matrices (A|B), (C|D) are row equivalent
If Ax=B, Cx=D are equivalent systems then the solutions are equal and if one of them are inconsistent then the other is as well.
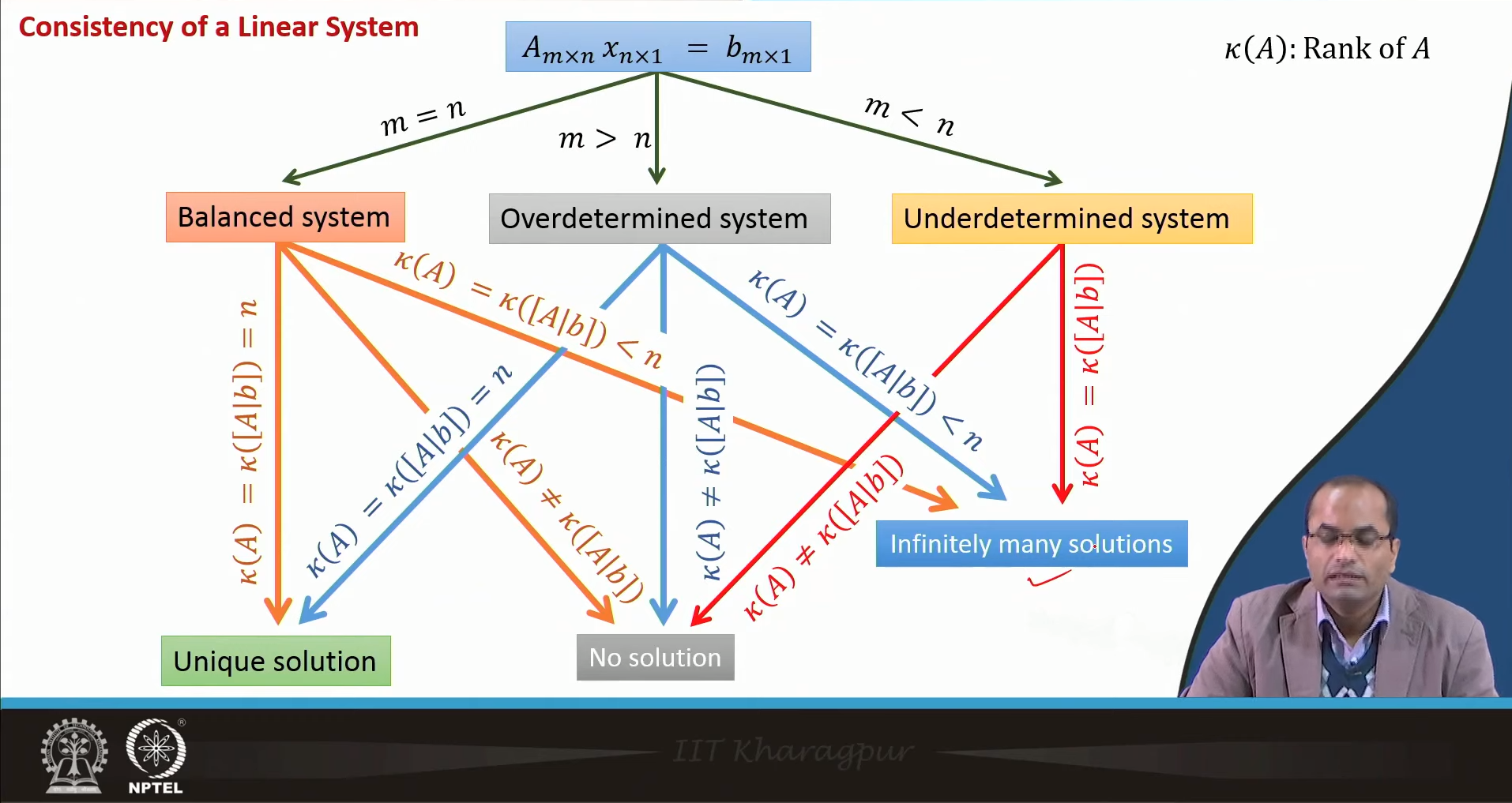
Existence and uniqueness of the solution #
- Consistent: $\text{rank}(A)=\bar A=r$
- Unique: r=number of unknowns
- Infinite: r< number of unknowns
- Inconsistent $\text{rank}(A)\ne \bar A$
For a Homogeneous System #
It cannot be inconsistent because $X=\vec{0}$ is always a solution, and so it can either have:
- 1 solution (zero vec.): rank(A)=number of unknowns
- infinite solutions: rank(A)< number of unknowns
But what is is the solution though? #
Direct Method #
Gauss elimination method is used to solve a system of linear equations.
Gauss Elimination: It’s the process of turning (A|B) into an echelon form (C|D) and solving the unknowns by substituting vars one by one.
Gauss Jordan Method: It’s when it’s reduced to row reduced echelon form (C|D). No need of back-substitution to find the solution.
Iterative Method #
Lecture 21: “Iterative Methods for Solving System of Linear Equations” - YouTube
Idea for deriving an iterative method:
$$ \begin{align*} Ax=B\\ (P-N)x=B\\ \text{P is a non singular matrix}\\ Px=Nx+B\\ x^{k+1}=Gx^{k}+HB\\ G: \text{ iteration matrix }=P^{-1}N;H=P^{-1} \end{align*} $$