Integral along virtual objects

Line integral #

Requires us to convert the line into a parametric curve to integrate $f(x,y,z)\cdot dr$

Surface integral #

Surface Area for Implicit & Explicit Surfaces // Vector Calculus - YouTube

$$ \begin{align*} dA: \text{elemental area of projection plane}\\ dS: \text{elemental area of surface}\\ \\ dS=\frac{|\vec \nabla F|}{|\vec\nabla F \cdot \hat p|}dA \end{align*} $$

p̂: normal vector to the plane that we’re projecting the surface against

Example #

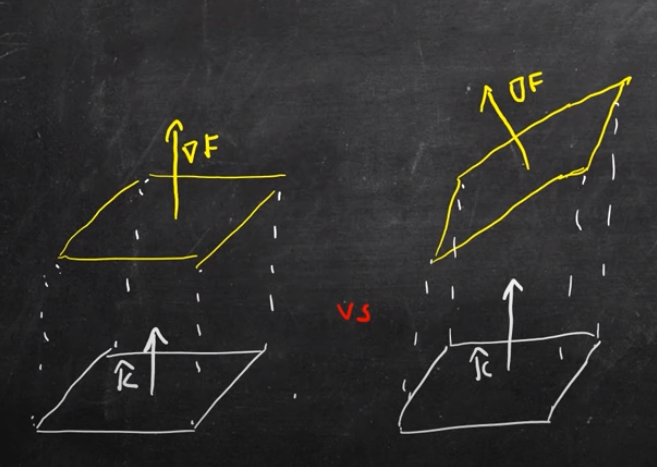
Projection plane: x-y plane

$$ \begin{align*} dA=dxdy\\ dS: \text{elemental area of surface}\\ \\ dS=\frac{|\vec \nabla F|}{|\vec\nabla F \cdot \hat k|}dA \end{align*} $$