Theorems and applications

Gauss Divergence Theorem #

Just two ways of looking at flux

Let F be a vector function having continuous partial derivatives in a volume V bounded by a closed surface S, then $$ \iint\limits _{S}\vec F\cdot \hat n dS = \iiint \limits _{V}(\vec \nabla\cdot\vec F)dV $$

Stokes Theorem #

Stokes’ theorem intuition | Multivariable Calculus | Khan Academy - YouTube

Just two ways of looking at total rotation

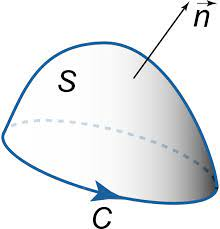
Let F be a function having continuous first order partial derivatives in a domain in space containing an open two sided surface S bounded by a simple closed curve C, then

$$ \int\limits_{C}\vec F \cdot \vec {dr}=\iint\limits_{S} (\text{curl }\vec F)\cdot \vec{dS} $$

$\vec{dS}=\hat n dS$

orientation of normal vector and C:

Green’s Theorem #

Green’s and Stokes’ theorem relationship | Multivariable Calculus | Khan Academy - YouTube

Just a special case of when the surface S is flat in the xy plane and we can construct $\vec F=<M,N,0>$

If M(x,y), N(x,y) be continuous functions having continuous partial derivatives in a region R of xy plane bounded by the closed curve C, then

$$ \oint \limits _{C}Mdx+Ndy = \iint \limits _{R}\left(\frac{\partial N}{\partial x}-\frac{\partial M}{\partial y}\right) dxdy $$