Compton Effect
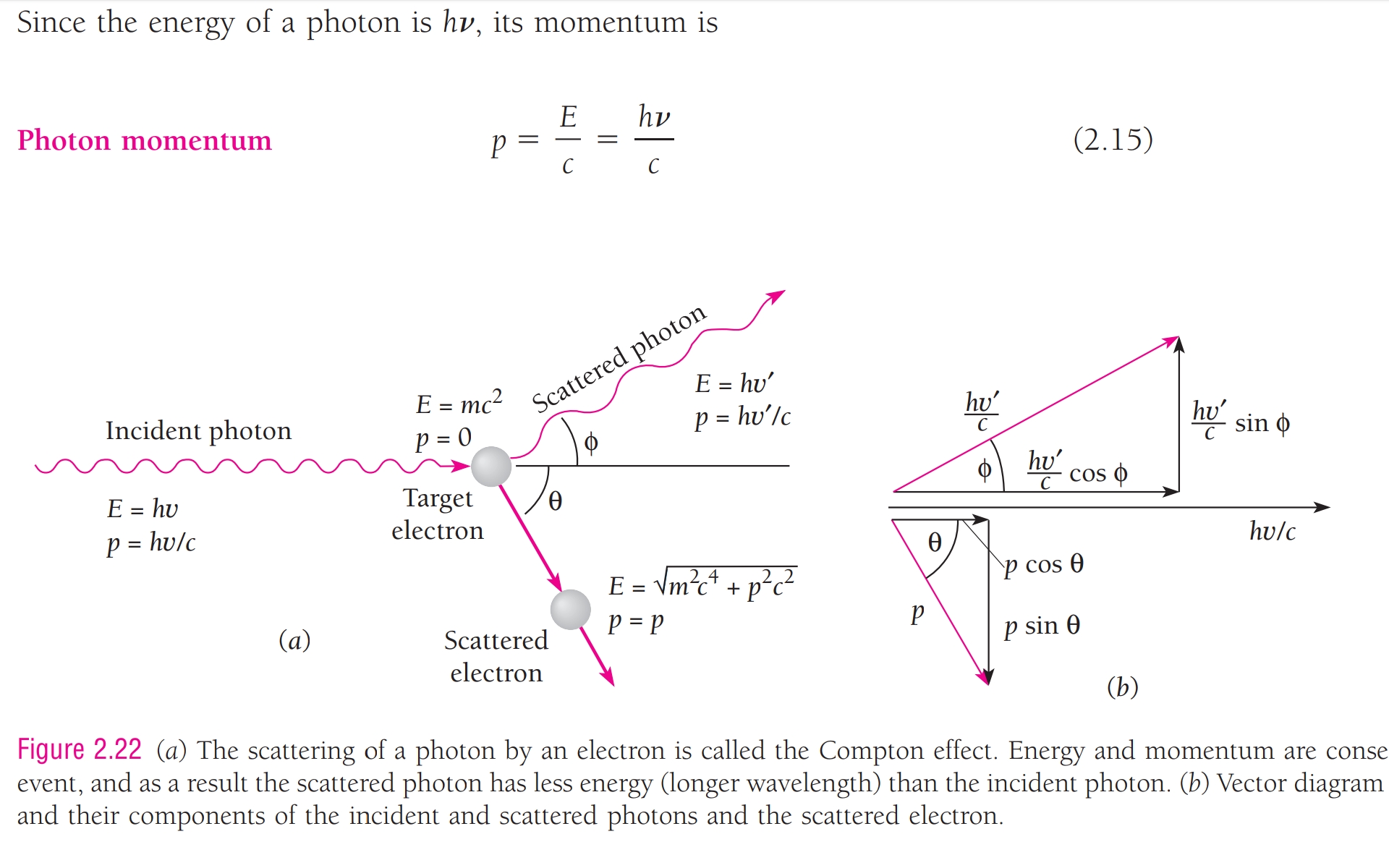
We can derive the relation by applying conservation of momentum and energy.
$$ \begin{align} \frac{hv}{c}+0=\frac{hv’}{c}\cos\phi+p\cos\theta\\ \frac{hv’}{c}\sin \phi=p\sinθ\\ \\ \\ E=KE+mc^2=\sqrt{m^2c^4+p^2c^2}\\ \text{or} \\ ((hv-hv’)+mc^2)^2=m^2c^4+p^2c^2 \end{align} $$
Relation:
$$ \begin{align} \lambda ‘-\lambda=\frac{h}{mc}(1-\cos\phi)\\ \text{Compton wavelength: } \lambda _C=\frac{h}{mc} \end{align} $$